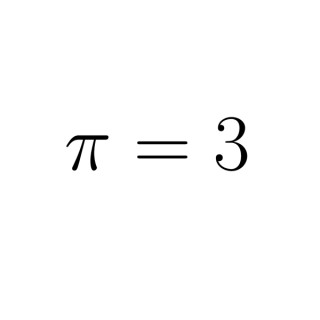Podcasts about bourbaki

Die Stiftung Bourbaki restauriert in der Stadt Luzern den grossen Baldachin über dem 112 Meter langen Panoramagemälde. Dafür müssen unter anderem 200 Kilo Stoff ausgetauscht werden. Für die technisch aufwändigen Arbeiten setzt das Museum auf Industriekletterer und investiert 800'000 Franken.  Weiter in der Sendung:  * Die Gemeinde Lachen kauft eine Liegenschaft des Elektrizitätwerks Lachen zurück. 

Fala Galera, neste epsódio, vamos falar sobre o modernismo na história da matemática. O modernismo na matemática é um movimento que surgiu no final do século XIX e início do século XX. Ele foi caracterizado por um esforço para colocar a matemática em bases sólidas e axiomáticas. Filosoficamente, esse movimento foi influenciado pelo positivismo, que defendia que o conhecimento é baseado na experiência. Os matemáticos odernistas acreditavam que a matemática deveria ser fundamentada em axiomas e teoremas que fossem logicamente demonstráveis. Quando começou? É difícil dizer exatamente quando o modernismo começou. Alguns historiadores apontam para o trabalho de Georg Cantor na teoria dos conjuntos, que começou na década de 1870. Outros apontam para o trabalho de David Hilbert, que começou na década de 1900. O modernismo na matemática é semelhante ao movimento modernista nas artes. Ambos os movimentos rejeitaram as formas tradicionais e buscaram novas formas de expressão. Ele teve um impacto em todas as áreas da matemática. Alguns exemplos incluem: O axioma da completude para os números reais (Hilbert) O axioma do infinito (Cantor) Os paradoxos da teoria dos conjuntos (Russeot) Construtivistas e não construtivistas O modernismo teve um impacto profundo na história da matemática. Ele levou a um desenvolvimento da matemática mais rigoroso e formal. No que chamamos hoje de bases sólidas .Os modernistas também acreditavam que a matemática deveria ser uma unidade. Eles buscavam unificar as diferentes áreas da matemática sob um conjunto de axiomas e teoremas. Um exemplo do esforço dos modernistas para unificar a matemática foi a teoria abstrata desenvolvida pelo grupo Bourbaki. Outro destaque foi Kurt Gödel mostrou que não é possível provar a consistência da matemática usando apenas axiomas e teoremas. Isso foi um golpe para os modernistas, que acreditavam que a matemática era umsistema consistente. Sejam todos bem vindos ao maravilhoso mundo da Matemática! Participantes: Marcelo Rainha ( Professor UNIRIO) Marcelo Amadeo (Professor Unirio) Ronan Fardim (CEDERJ/UNIRIO - Polo Belford Roxo) Juliana Almeida (UFF) Edição e sonorização: Jorge Alves (UNIRIO) Leandro Rodrigo (UNIRIO) Dicas culturais: Hotel de Hilbert: https://www.youtube.com/watch?v=pjOVHzy_DVU&t=4s A Brieff History of Mathematics: https://open.spotify.com/show/2Gde5u4UPKOEwqmqcKIScH?si=8b80bd6c3f4f43fc Mariguela Plato's Ghost: The Modernist Transformation of Mathematics Referências: Gray,J.J. ; Ferreirrós, J. ; The Archteture of Modern Mathematics, Oxford, 2006, Cap Introcuction Gray,J.J.; Modernism in mathematics as a cultural phenomenon, 2006. Todo material dos jogos criados e elaborados pela equipe Jogos & Matemática está disponível GRATUITAMENTE no nosso site: ⁠⁠⁠⁠⁠⁠⁠https://www.jogosematematica.com.br/ ⁠⁠⁠⁠⁠⁠⁠ Acompanhem nossas mídias e não perca nenhuma novidade! :) Inscreva-se no nosso canal do YOUTUBE: ⁠⁠⁠⁠⁠⁠⁠https://www.youtube.com/c/JogosMatemática⁠⁠⁠⁠⁠⁠⁠ Curta e siga nossa página no FACEBOOK: ⁠⁠⁠⁠⁠⁠⁠https://www.facebook.com/jogosematematica⁠⁠⁠⁠⁠⁠⁠ Siga-nos no INSTAGRAM:⁠⁠⁠⁠⁠⁠⁠ ⁠⁠⁠⁠⁠⁠⁠⁠⁠⁠⁠⁠⁠⁠https://www.instagram.com/jogosematematica⁠⁠⁠⁠⁠⁠⁠ Siga-nos no SPOTIFY: ⁠⁠⁠⁠⁠⁠⁠https://open.spotify.com/show/65i8uB46F07p4WaTYqkb5Q?si=AtewFx8vRWqWnfHWvt-xKw&nd=1⁠⁠⁠⁠⁠⁠⁠ Visite o nosso BLOG:⁠⁠⁠⁠⁠⁠⁠ ⁠⁠⁠⁠⁠⁠⁠⁠⁠⁠⁠⁠⁠⁠https://jogosematematica.wordpress.com⁠⁠⁠⁠⁠⁠⁠ Dúvidas, críticas, sugestões? Escrevam para: jogosematematica@gmail.com A EDUCAÇÃO NO BRASIL PRECISA DE TODOS NÓS!!! JUNTOS SOMOS MAIS FORTES!!! MUITO OBRIGADO A TODOS!!!

Ministero della Pubblica Istruzione - Roma (31/05/23) --- Send in a voice message: https://podcasters.spotify.com/pod/show/vito-rodolfo-albano7/message

With mathematical physicist Ian Jauslin, we explore both scientific and personal topics, including: - whether our universe could be nonlocal - why not to put people and concepts into boxes - what can math look like when approached organically - how to constantly keep learning   Startovač: https://www.startovac.cz/patron/misto-problemu/ FB page: https://www.facebook.com/mistoproblemu Web: https://www.mistoproblemu.cz/   Timestamps: (00:00) introduction (02:46) bosons and superfluidity (05:46) crystallization (17:30) math/physics interplay (20:48) Bell's inequality (34:12) consequences of nonlocality (39:04) quantum cryptography (45:12) putting people and concepts in boxes (52:52) Bourbaki vs. organic education (1:01:28) applicability and approach to research (1:06:53) outreach (1:16:30) curiosity (1:21:25) efficiency, vim, and keyboard layouts (1:30:07) failures in research, time management (1:37:24) easy life and definition of success (1:41:40) problem-solving strategies (1:45:52) a final plea   Links: - Ian's webpage: http://ian.jauslin.org/ - YouTube channel: https://www.youtube.com/channel/UC5OD3zd3Ds0Syf6s6cYemIw - Einstein-Podolsky-Rosen paper: https://iep.utm.edu/wp-content/media/epr-pdf.pdf - Nicolas Bourbaki: https://en.wikipedia.org/wiki/Nicolas_Bourbaki - Bell's inequality: http://scholarpedia.org/article/Bell%27s_theorem - vim: https://www.vim.org/ - Committee of Concerned Scientists: https://concernedscientists.org/

Bảo Châu NgôCollège de FranceFormes automorphes (chaire internationale)Année 2022-2023Théorie géométrique des représentationsSéminaire - Philip Boalch : First Steps in Global Lie Theory: wild Riemann surfaces, their character varieties and topological symplectic structuresRésuméI'll describe some of the story leading up to the construction of the topological symplectic structures (P.B. Oxford thesis 1999, Adv. Math. 2001) and subsequent evolution leading to the general, purely algebraic approach (B. 2002, 2009, 2014, B.-Yamakawa 2015). They generalise the holomorphic version of the symplectic structures of Narasimhan, Atiyah- Bott, Goldman involving the topological fundamental group. Our approach gives a TQFT approach to moduli of meromorphic connections on curves, involving Lie group valued moment maps.The right point of view seems to be to generalise the notion of Riemann surface to the notion of wild Riemann surface, in the spirit of Weil's 1957 Bourbaki talk, and view these symplectic varieties as their character varieties (in the spirit of Weil's 1948 text "Sur les courbes algébriques et les variétés qui s'en déduisent"). The simplest irregular example (involving the wild fundamental group) underlies the Drinfeld- Jimbo quantum group (and deformations of the underlying wild Riemann surface explain the natural G-braid group action of Lusztig). Classification of these varieties, as "global analogues of Lie groups", is still at a quite elementary stage, but a rich theory of Dynkin diagrams exists for many examples.If time permits I'll describe how these two-forms fit together with the Bottacin-Markman Poisson structure on the meromorphic Higgs bundle moduli spaces to give the wild nonabelian Hodge hyperkahler manifolds (Biquard-B. 2004). Surprisingly these hyperkahler metrics are often complete even though the corresponding harmonic maps have infinite energy. The simplest examples, certain hyperkahler four- manifolds, are the "spaces of initial conditions" of the Painlevé equations. Painlevé knew his equations were deformations of equations for elliptic functions, and so we can now see this "Painlevé simplification" as a hyperkahler rotation, from meromorphic connections to meromorphic Higgs bundles. Not only does this story encompass many famous classical integrable systems like the Lagrange top (2 poles of order 2), and those studied by Mumford (in Tata lectures on Theta II), but several of these Painlevé integrable systems were used in Seiberg-Witten's 1994 solution of 4d N=2 super Yang-Mills theory for SU(2), and one of the higher rank generalizations, introduced by Garnier in 1919 (the simplified Schlesinger system), underlies the famous Gaudin model. It was solved by Garnier in terms of abelian functions by defining spectral curves, a method rediscovered in the soliton literature in the 1970s (see e.g. Adler-Van Moerbeke 1980, Linearization of Hamiltonian systems, Jacobi varieties and representation theory, p.337, or Verdier's 1980 Séminaire Bourbaki), before being generalised by Hitchin to the case where the base curve has genus >1.Philip BoalchPhilip Boalch1991-1997: Cambridge University (B.A, Part 3, start of PhD at DPMMS)1993: summer employment drawing optical solitons (GEC Hirst research lab.)1997-1999: Oxford University, D.Phil (N. Hitchin)1999-2001: Post-doc Trieste (B. Dubrovin, M.S. Narasimhan)2001-2002: Post-doc Strasbourg (O. Biquard)2002: recruté par le CNRS2002-2003: Post-doc Columbia, New York (I. Krichever)2003-2013: CNRS, ENS Ulm2013-2014: IHES2014-2019: Orsay2019-: IMJ-PRG, Université Paris Cité

Du willst deine Lieblingsfilme auf Grossleinwand sehen? Genau das organisiert Stephan mit seiner Kino On Demand Plattform "The Ones We Love".Auf The Ones We Love kannst du helfen, deine Lieblingsfilme für eine oder mehrere Vorstellungen wieder ins Kino zu bringen. Du kannst entweder einen auf der Plattform vorhanden Film wählen, oder einen eigenen Film vorschlagen. Anschliessend findet ein Voting für ein spezifisches Datum und ein Kino statt. Bis der Countdown abläuft, kann und soll fleissig gevoted werden. Du kannst so oft wählen wie du willst, pro Film und Stadt aber nur einmal. Der Film, welcher nach Ablauf des Contdown auf Platz 1 steht, wird gezeigt. Anschliessend kann die Vorstellung gebucht werden. Die Vorstellungen sind nicht nur den Votern vorbehalten. Sie stehen selbstverständlich allen interessierten Kinoliebhabern offen. The more the merrier!Im Moment werden die Filme in den Kinos Bourbaki in Luzern, cineCamera in Bern, Kinepolis in Schaffhausen, Kinokoni in Olten, Rex in Thun und Riffraff in Zürich gezeigt.Hier geht's zur Plattform: https://www.theoneswelove.ch/

Venerdì 4 novembre 2022 il gruppo di lavoro Nicoletta Bourbaki – nelle persone di Luca Casarotti e Benedetta Pierfederici – ha presentato alla libreria Modo Infoshop di Bologna il libro La morte, la fanciulla e l'orco rosso. Il caso Ghersi: come si inventa una leggenda antipartigiana (Alegre, 2022). Chi ha manipolato, e come, e quando, la storia dell'uccisione della delatrice repubblichina Giuseppina Ghersi? Quel che è certo è l'obiettivo: farne una storiaccia morbosa, in bilico tra horror e porno. Una storia che vorrebbe dire qualcosa sui partigiani, mentre dice molto di più sui fascisti che l'hanno inventata. A introdurre l'evento e dialogare con NB c'era Wu Ming 1. Buon ascolto.

Following our previous episode on Richard P. Gabriel's Incommensurability paper, we're back for round two with an analysis of what we've dubbed the Worse is Better family of thought products: The Rise of Worse Is Better by Richard P. Gabriel Worse is Better is Worse by Nickieben Bourbaki Is Worse Really Better? by Richard P. Gabriel Next episode, we've got a recent work by a real up-and-comer in the field. While you may not have heard of him yet, he's a promising young lad who's sure to become a household name. Magic Ink by Bret Victor Links The JIT entitlement on iOS is a thing that exists now. Please, call me Nickieben — Mr. Bourbaki is my father. A pony is a small horse. Also, horses have one toe. Electron lets you build cross-platform apps using web technologies. The apps you build in it are, arguably, doing a bit of "worse is better" when compared to equivalent native apps. Bun is a new JS runner that competes somewhat with NodeJS and Deno, and is arguably an example of "worse is better". esbuild and swc are JS build tools, and are compared to the earlier Babel. The graphs showing the relative lack of churn in Clojure's source code came from Rich Hickey's A History of Clojure talk. To see those graphs, head over to the FoC website for the expanded version of these show notes. Some thoughts about wormholes. futureofcoding.org/episodes/059See omnystudio.com/listener for privacy information.

En esta xTALK.AI tenemos el placer de entrevistar a Carlos Alfonso Ruiz Guido del Colegio de Matemáticas aplicadas Bourbaki. Hablamos de Matemáticas, Data Science, Datos, de Inteligencia Artificial, de formación, tendencias... pero también presentamos una iniciativa de proyectos de bases de datos muy interesante.Una xTALKS.AI imperdible y super interesante.Colegio de Matemáticas Bourbaki : LinkedInEnlaces relacionados:Paper GROKKING: GENERALIZATION BEYOND OVERFITTING ON SMALL ALGORITHMIC DATASET Support the show

Das stattkino Luzern gehört zum Kulturleben der Stadt und der Region Luzern! Im Bourbaki eingemietet, neben den Sälen des Kino Bourbaki, befindet sich das Stattkino Luzern. Das Kino ist ein nicht kommerzielles Programm-Kino mit der Zielsetzung, jene Filme vorzuführen, die im gewerblich orientierten Kinoangebot entweder nicht oder nicht mehr enthalten sind. Es setzt sich ein für engagierte und oft auch unbequeme Filme, die sonst vielfach gar keinen Platz mehr haben in der Luzerner Kinoszene. Leimgruber macht ein Programm, wie es kein einziges Kino weit und breit sonst macht: «Mich interessieren die nicht-kommerziellen Filme. Das Mainstream-Kino ist nie meine Heimat gewesen.» (Luzerner Zeitung)Mehr über Peter erfährst du in diesem gelungenen Bericht von Pirmin Bossart: https://www.luzernerzeitung.ch/kultur/stattkino-luzern-peter-leimgruber-ein-kaempfer-fuer-anspruchsvolle-filme-ld.89081 Und das aktuelle Programm vom Stattkino findest du hier: https://www.stattkino.ch

Welcome back to Hattie Talks, after a long 10 month break, for episode 1 of Hattie Talks: Mathematics! Today, I'm talking about the mathematician who never existed, Nicolas Bourbaki - in under 10 minutes. Enjoy!

Daniela Küttel ist Mitglied der GL der Neugass AG und seit Jahren in der Kino-Landschaft der Schweiz zuhause. Die Neugass AG betreibt die Kinos Riffraff und Houdini in Zürich und das Kino Bourbaki in Luzern. Die Kinos zeichnen sich mit einem feinen Programm jenseits des Mainstreams und der Blockbuster aus und sprechen so auch ein anderes Publikum an. Was sich aus zu zeichnen scheint, da das Kino Bourbaki schon sehr bald das letzte Kino (neben dem Stattkino, aber dazu in ein paar Wochen mehr) in der Stadt Luzern sein wird, nachdem alle anderen Kinos noch dieses Jahr ihre Tore schliessen werden.Der Erfolg der Neugass Kino AG basiert auf einem ausgewählten Filmprogramm, das sich an ein Publikumssegment richtet, welches neben Unterhaltung auch eine geistige Herausforderung sucht. Die Neugass Kino AG legt zudem grossen Wert auf ergänzendes Angebot, Auftritt und Umfeld.Mehr Infos zu den Betrieben findest du hier: https://www.neugasskino.ch

Alfonso estudió matemáticas en la UNAM, en la Université d'Orsay y en Oxford University. Durante su carrera ha visitado y expuesto su trabajo en diversas instituciones tales como UCLA, Universität Münster, Notre Dame University, Institute Henri Poincaré, IHES, CIRM, Sophus Lie Conference Centre, CIMAT, University of Miami entre otros. Actualmente es Director del Colegio de Matemáticas Bourbaki y dedica su tiempo a convertirlo en un centro de enseñanza e investigación de primer nivel. Este podcast es presentado por X-DATA, el estudio de análisis y visualización de datos más efectivo en México, es el manual que necesitas para potenciar tus negocios y proyectos a través de los datos. Learn more about your ad choices. Visit megaphone.fm/adchoices

durée : 00:03:43 - Le Pourquoi du comment : histoire - par : Gérard Noiriel - De la fiction au réel, une aventure intellectuelle qui illustre un côté admirable de l'activité scientifique.

Nicola Bourbaki es una genialidad creativa además de un referente dentro de las matemáticas. A parte de su obra, su vida es digna de conocimiento y difusión. Porque en tantas cosas, no todo es lo que parece. Recuerda que tienes la versión blog disponible en anesortigosa.es

1934 treffen sich sechs junge französische Mathematiker im Café Copulade und beschließen die Grundlagen der Mathematik abgeschlossen und stringent neu aufzuschreiben. Sie wollen die Lehrbuchsituation verbessern.

Im eisig-kalten Februar 1871 kamen 87'000 französische Soldaten in die Schweiz – nicht als Aggressoren, sondern als Geschlagene im deutsch-französischen Krieg. Die Soldaten der Bourbaki-Armee wurden von Deutschland im französischen Jura regelrecht in die Enge getrieben. Ihnen blieb kein anderer Ausweg, als in der Schweiz Zuflucht zu suchen, sich internieren zu lassen. Die Soldaten schleppten sich innerhalb weniger Tage im Neuenburger und Waadtländer Jura über die Grenze: ausgehungert, krank, verletzt, mit Erfrierungen. In der Schweiz wurden sie generalstabsmässig auf über 200 Gemeinden in fast allen Kantonen verteilt. Dort blieben sie während sechs Wochen. Die Schweizer Behörden waren ebenso gefordert, wie die Bevölkerung. Von allen Seiten war die Hilfsbereitschaft gross. «Für die Schweiz war die Internierung der Bourbaki-Armee ein Präzedenzfall für die bewaffnete Neutralität», sagt in der «Zeitblende» der Historiker Patrick Deicher. Er hat die Bourbaki-Internierung erforscht und bringt sie uns vor dem monumentalen Bourbaki-Panorama-Gemälde in Luzern näher.

Max Karoubi is a Professor Emmeritus at the University of Paris 7, working in K-theory and algebraic topology. In this interview, Max shares warm memories about Grothendieck and the Bourbaki group, discusses math studies in Northern Africa and highly recommends doing research in collaborations. Max' webpage: https://webusers.imj-prg.fr/~max.karoubi/ Photo: from Max' webpage 0:00​ teaser 0:43​ getting into math in Northern Africa 5:33​ getting a family helped to do math 9:12​ PhD under Cartan and Grothendieck 13:05​ Grothendieck: naive genius 16:53​ Karoubi as a name for math terminology 19:18​ new foundations of hermitian K-theory 22:20​ why write math in french 26:33​ founding European Congress of Mathematics 29:30​ collaborators are the best 34:35​ the importance of teaching 38:53​ why french people are arrogant 42:26​ RIP good jobmarket times 44:33​ how we can help math in developing countries 46:44​ traveling to USSR in 1961 48:58​ please don't boycott ICM! 51:35​ you cannot do math alone 55:58​ wish for young mathematicians

(00:00:32) Frank Braun ist Programmleiter der Kinohäuser Riffraff, Houdini und Bourbaki in Zürich und Luzern. Gerade wurde er mit dem Prix d'Honneur der Solothurner Filmtage ausgezeichnet, dies für sein Engagement für die Schweizer Filmszene. Er spricht über Film und Corona und den Winter im Bild. Weitere Themen: (00:13:54) Ausgezeichnet für seine Lebendigkeit: Der Wakker-Preis geht in diesem Jahr an Prangins am Genfersee. (00:17:43) Vorläufig mit Bundesgeld gerettet: Das Gosteli-Archiv, das Dokumente zur Geschichte der Frauenbewegung sammelt. (00:21:26) Erfolg dank «colorblind casting»? Die Netflix-Serie «Bridgerton» begeistert weltweit zahlreiche Fans. (00:25:15) Die «Lockdown Collection» versammelt 25 Kurzfilme aus allen Sprachregionen der Schweiz. Wie setzen Filmschaffende die Pandemie um? (00:29:27) «Kurze Geschichten zur langen Pandemie». Unter diesem Motto haben AutorInnen für Schweizer Radio SRF kurze Hörstücke zur Pandemie geschrieben – humorvoll, reflektierend, kritisch. Teil 1: Emanuel Bundi

Nicolas Bourbaki a su révolutionner en profondeur les mathématiques du XXe siècle, en France et dans le monde entier. Ses onze volumes de mathématiques ont su proposer un regard neuf sur la discipline, accompagné d'une révision des fondamentaux et un travail colossal de clarification et de réorganisation. Pourtant, Nicolas Bourbaki n'a jamais existé.Derrière son nom se cache en réalité une société secrète de brillants mathématiciens, fondée en 1935. Leur objectif : exposer les mathématiques depuis leur début en réalisant un grand coup de ménage. L'héritage presque centenaire de Nicolas Bourbaki est aussi important aujourd'hui que l'histoire de ses origines est fascinante.Pour aller plus loin :La biographie de Nicolas BourbakiGrothendieck : l'Albert Einstein des mathématiques du XXe siécle est décédé

Nicolas Bourbaki a su révolutionner en profondeur les mathématiques du XXe siècle, en France et dans le monde entier. Ses onze volumes de mathématiques ont su proposer un regard neuf sur la discipline, accompagné d'une révision des fondamentaux et un travail colossal de clarification et de réorganisation. Pourtant, Nicolas Bourbaki n'a jamais existé.Derrière son nom se cache en réalité une société secrète de brillants mathématiciens, fondée en 1935. Leur objectif : exposer les mathématiques depuis leur début en réalisant un grand coup de ménage. L'héritage presque centenaire de Nicolas Bourbaki est aussi important aujourd'hui que l'histoire de ses origines est fascinante.Pour aller plus loin :La biographie de Nicolas BourbakiGrothendieck : l'Albert Einstein des mathématiques du XXe siécle est décédé Voir Acast.com/privacy pour les informations sur la vie privée et l'opt-out.

programmateur RiffRaff, Houdini et Bourbaki entre autres Pour regarder l'émission, c'est par ici : https://www.youtube.com/watch?v=n8qrMqaMtY0&t

Episode: 1829 Multiple authors, multiple problems: Whose work is this?  Today, whose work is this?

Sans doute le seul à maîtriser la totalité du champs de cette discipline. Ses publications ont eu une influence considérable sur l’enseignement des maths. C’est aussi lui qui a inventé le symbole du rond barré pour désigner un ensemble vide. Et ça tombe bien, puisque Nicolas Bourbaki n’a jamais existé.   Avec Baptiste Zapirain et Charles Trahan   

Il primo festival Contrattacco è stato organizzato dal Vag61 di Bologna ed Edizioni Alegre. Si è svolto al Vag61 dal 9 all'11 novembre 2018. Durante la terza giornata Nicoletta Bourbaki, gruppo di lavoro sul revisionismo storiografico, le bufale storiche in rete e le ideologie neofasciste. Il gruppo presenta il proprio ebook “Questo chi lo dice? E perché?”: una guida per riconoscere e smontare le bufale fasciste.

A Treviso il centro sociale Django, da tempo sotto attacco, invita il gruppo di lavoro Nicoletta Bourbaki a presentare la sua guida alle bufale storiche in rete Questo chi lo dice? E perché?La destra cittadina, poi regionale, poi nazionale insorge: dichiarazioni di fuoco! Paginate di giornali! Servizi televisivi!… contro chi? Contro i «negazionisti delle foibe»!!! Si esprimono rabbiosi i soliti personaggi, da Elena Donazzan in giù, e si chiede, anzi, si esige a gran voce l’annullamento della serata.Un’allucinazione collettiva o, più probabilmente, una menzogna consapevole da poter usare contro il Django. O forse entrambe le cose.Sia il Django sia Nicoletta Bourbaki tengono i nervi saldi, e viene anche un’idea su come gestire la serata.Serata che, in barba ai frustrati fascioleghisti, riesce molto bene.Su Medium, Nicoletta Bourbaki ricostruisce gli avvenimenti e il clima dei giorni scorsi, e fa notare come ormai basti gridare «foibe!» per poter invocare la censura nel consenso (o almeno non-dissenso) generale.https://medium.com/@nicolettabourbaki/django-unfoibed-8796878bb075L’audio della serata è in questo stesso podcast. Buon ascolto.

«Le dita nella presa», trasmissione di approfondimento tecnologico a cura del collettivo AvANa, in onda su Radio Onda Rossa, Roma. Puntata del 23 settembre 2018. Nuovo ciclo sull'attendibilità dell'informazione in rete. In questa puntata, focus su Wikipedia con Luca Casarotti del collettivo Nicoletta Bourbaki. I limiti dell'"enciclopedia libera", il metodo di indagine storiografica che Nicoletta utilizza, esempi dei metodi che i revisionisti usano per presentare una lettura distorta della storia su Wikipedia.

SynTalk thinks about theories & theorizing, while constantly wondering whether theories are explanatory as well as speculative (‘what-if’). Are all theories, in a sense, artistic creations and inventions (rather than discoveries)? Can we take the human out of the equation? The concepts are derived off / from Euclid, Newton, Leibniz, Alexander Pope, Robert Hooke, Boole, Faraday, Maxwell, Gauss, Hilbert, Godel, Bourbaki, Abraham Robinson, Weinberg, Stanley Fish, Lawvere, & Stephen Wolfram, among others. How all physical theories have a desire to predict & look into the future. How mathematical theories, however, do not need to predict and have no role for evidence. Further, how theories in literature are an attempt to explain the process of interpretation? Are there theories that are finished pieces of work (test: when all true statements are provable)? Are some theories destined to be incomplete? Will we ever have a complete theory for poetry? Is all of mathematics just a theory? Do all theories (real numbers, classical mechanics) have limits? Is everything that is there to be known about a triangle now known? How a theory comes to be conceived in areas far far removed from available knowledge, via a leap of imagination or (even) an act of faith. How ‘non-logical axioms’ when put into the magical black box of ‘logic’ churns out a list of ‘provable statements’. How crystalline & elegant axioms are often identified after years of calculations. Can we, for instance, axiomatize the notion of space or theorize about some currently ill understood domains of gravitation at the largest scale? How logic specifies a grammar for construction. How double negation may not work in some systems (what is not true is not necessarily false). May the idea of the observable or the ways of seeing itself be theoretical constructions? Can finished theories have parallel ways of thinking (say, lines of force, fields of force, or electromagnetic potential)? The links between theoreticity and abstraction, & is (even) man a theory (‘the proper study of mankind is man’?). Are (electrical) circuit laws completely autonomous of the fundamental Maxwell equations? Are Laws the robe and Theory the wardrobe? The links between dog star, functor, earthquake, QCD, ‘mortal grossness’, Nile floods, fluxions, video games, chariot, White Males, synthetic differential geometry, love-dove-&-shove, & the salt doll. How theories wax & wane with the consensus and dissensus of interpretive communities. Are there universal truths? Can we simulate the answer to any question with extremely efficient computation without theories? Will theory itself come to an end in the long run? The SynTalkrs are: Dr. Partha Pratim Ghosh (mathematics, ISI, Tezpur), Prof. Pramod K. Nayar (literature, University of Hyderabad, Hyderabad), & Prof. Urjit A. Yajnik (physics, IIT Bombay, Mumbai).

Cycle de conférences organisées par la Bibliothèque nationale de France et la Société mathématique de France. Conférence du 14 janvier 2015. Conférences organisées à l'attention du grand public, des professeurs du second degré et des lycéens et étudiants, les conférenciers partent d'un texte, ou d'un corpus de textes, et montrent en quoi ce texte les a influencés personnellement et a conduit à des recherches contemporaines

Cycle de conférences organisées par la Bibliothèque nationale de France et la Société mathématique de France. Conférence du 14 janvier 2015. Conférences organisées à l'attention du grand public, des professeurs du second degré et des lycéens et étudiants, les conférenciers partent d'un texte, ou d'un corpus de textes, et montrent en quoi ce texte les a influencés personnellement et a conduit à des recherches contemporaines.

Cycle de conférences organisées par la Bibliothèque nationale de France et la Société mathématique de France. Conférence du 14 janvier 2015. Conférences organisées à l'attention du grand public, des professeurs du second degré et des lycéens et étudiants, les conférenciers partent d'un texte, ou d'un corpus de textes, et montrent en quoi ce texte les a influencés personnellement et a conduit à des recherches contemporaines.

The thirteenth lecture in Dr Joel Feinstein's G11FPM Foundations of Pure Mathematics module covers Informal definition of function, along with associated notation and terminology, including domain, codomain, argument, value, and notation. Definition of the graph of a function, with notation and examples. Formal definition of function (Bourbaki approach). These videos are also available on YouTube at: https://www.youtube.com/playlist?list=PLpRE0Zu_k-BzsKBqQ-HEqD6WVLIHSNuXa Dr Feinstein's bl

En 1939, un matemático desconocido, de apellido Bourbaki, comenzó la publicación de un ambicioso tratado, titulado Elementos de matemática, con la pretensión de compendiar la totalidad de las matemáticas como una materia unitaria, de manera que las relaciones entre las distintas ramas de la disciplina quedaran claramente visibles. Por eso el título del tratado se refiere a la matemática, en singular. Ese año se publicó parte del primer volumen, el Fascículo de resultados de la Teoría de conjuntos. En 1998, Bourbaki publicó Profundidad, regularidad, dualidad, último capítulo del volumen dedicado al Álgebra conmutativa y última sección publicada hasta la fecha. ¿Quién es ese longevo matemático, cuya carrera se ha extendido durante sesenta años?

Our new book, "Loving and Hating Mathematics," is about the emotional, social and political aspects of mathematical life. A major chapter tells of mathematical communities, such as Gottingen in the early 20th century, Bourbaki in Paris, and the Courant Institute in New York. The creation of such a productive community often depends on the leadership and vision of a vital, charismatic figure How the community continues and endures depends on how its members internalize and develop that vision.

This ten part history of mathematics from Newton to the present day, reveals the personalities behind the calculations: the passions and rivalries of mathematicians struggling to get their ideas heard. Professor Marcus du Sautoy shows how these masters of abstraction find a role in the real world and proves that mathematics is the driving force behind modern science. Today, the mathematician that never was, Nicolas Bourbaki. A group of French mathematicians, working between the two world wars and writing under the pseudonym Nicolas Bourbaki transformed their discipline and paved the way for several mathematical breakthroughs in the 21st century.Producer: Anna BuckleyFrom 2010.